TSO and TeeClub

Date: Tue, 23 Mar 2004 02:18:22 -0800 (PST)
From: Francis F Steen <steen@commstds.ucla.edu>
To: Mari Sian Davies <msdavie1@cs.uchicago.edu>
Subject: TSO and TeeClub

Hi Mari,

I spent the day trying to understand what we mean by strategy learning and wrote the following -- it's 6000 words and probably almost none of it would fit in a Sims article, but it does some really neat stuff on strategies. The idea is that what attracts people to games is strategy learning, and we need a theory of what that means. This would help us understand why the Sims Online is not that attractive -- in brief, I world argue it doesn't provide a world that is sufficiently predictable for the user to be able to develop strategies. Or rather, the predictability the user can take advantage of does not tap into the kinds of motivations people have for relating to others.

A significant part of this is that the Sims reduces the significance of others to an instrumental function. This is perhaps the most striking feature of the game. It's interesting that such instrumentality is not inadequate in the offline version, where the people are all sims anyway. (My first impulse, for instance, was to see if I could kill one off, after having read about the various tricks that could be used to accomplish this.) In the online world, on the other hand, it is profoundly unsatisfactory to treat others as having only instrumental significance. This is in part because we feel that others in fact have a value in themselves (the basis of ethics), and moreover that we feel that it is in the recruitment of another's thinking, feeling, creativity, and enthusiasm that really fun projects can be accomplished.

The trap, then, is in the transition from the offline Sims, which allows a certain combinatorial exploration that is similar to the card game I beat to death (I better watch my metaphors) below, to the online sims, which requires a different order of rules. What is the difference? In brief, the difference is that the offline Sims simply needs to provide an environment that is at once sufficiently complex and sufficiently predictable for a single player to develop strategies (see below for what I mean by strategies). TSO, in contrast, needs to provide not only rules that make the environment predictable (thus allowing the development of strategic thinking), but rules that make individuals predictable to each other in a manner that leaves their creativity intact. Now this is a hard problem, but human societies have solved it innumerable times.

Such rules need to be prescriptive rules -- that is to say, deontic or moral. They need to be rules that belong in the category "social contract" -- and violators of the rules need to be punished. TSO appear to be devoid of deontic rules -- there is nothing in the game that suggests what it means to be a good person in the game, a good citizen. Is this the source of the spectacular failure of the Sims, and is the absence of deontic rules the reason we're seeing so much talk about the Sims trying to deal with antisocial behavior?

The reason people need deontic rules is that people need to be able to predict each other without removing the creativity of the individual. You can create interactions that simply remove originality, as in army discipline, and this lets you predict what the other is going to do. The Sims have translated rules of behavior that works for Sims (offline, pretend people) to the online world, making the online world predictable, but in a manner that eviscerates their creativity. So deontic rules is the solution to the hard problem of making people predictable without removing their freedom and creativity. (I'm just groping my way here of course.)

You need deontic rules to constrain what people do -- for instance, you need rules that tell you how to treat people that belong to your group. (I've been talking with Dwight Read about this in the case of hominid evolution, kinship groups, etc.) If you know what group you belong to, and you know what the deontic rules are within that group, then you can join the group and rely on everyone adhering to those rules. This makes the interactions even between individuals predictable, and thus you can get real collaboration going fast. If you violate the norms, you're punished in some way -- the group needs to have ways of punishing people. Incidentally, all of this is spelled out in well-known "rules for creating successful online communities" (I assigned them to my class).

OK, so that's the argument. In order to make it worthwhile to play with others, you need to define groups that adhere to deontic rules (norms, prescriptive rules), and that provide the benefits of collaboration to those who adhere to these rules, and that penalizes people who violate the rules. If you can't do this, you'll fail to tap into the creative power of collaboration, in which individuals are treated as goals in themselves. If you fail to do this, you're reduced to treating people instrumentally, as goals to something else, and this makes for a profoundly boring game -- or worse, a vicious game in which people are reliably exploited, and without recourse.

This is a very straightforward and yet reasonably powerful critique. The failure is particulary vividly illustrated by the spread of vice in TSO -- prostitution, abuse of newbies, and various expressions of the absence of norms -- expressions of people treating others instrumentally. I bet we can also find some evidence of this in the footage and journals, as well as in your own experiences. The presidental election is explicitly an attempt to root out vice and protect the weak; the question will be whether a group can establish itself in TSO that operates according to norms and that provides tangible benefits and advantages to its "members" -- that is to say, whether the software that generates TSO is capable of supporting normed communities, since it is clear it was designed without any such function in mind.

Now, the section on strategy learning below is relevant only to the extent that it illuminates where TSO comes from, namely The Sims, and it's not even all that useful for this purpose, since it doesn't use examples from the Sims to illustrate the theory. Instead it uses a solitaire game, chosen because it represents a really well-defined problem space where the basic mechanisms are particularly easy to describe, unencumbered by the distractions of a more complex game like The Sims.

Let me know if you think the basic thrust makes sense -- the stuff about the lack of the ability within TSO to form a distinct group of people that identify themselves through their adherence to a set of deontic rules, and moreover the lack of an incentive system that permits such communities to be successful.

Best wishes,
Francis

Strategy learning

What you have in games is a set of agents and a set of possible actions. In general, games are hyperintelligible or simplified; they are designed to provide the player with an optimal rather than a maximal challenge.

Games are simulations of life, in the form of hyperintelligible abstractions. A good game will abstract some regularity that occurs in real life, destilling it down to a few simple principles. These principles are built into the game and need not be explicitly stated; the player is likely not even aware of them [*this is a good research question: how would you describe the world that The Sims simulates? On which principles is it based?]

The key feature of games is that an invarient set of agents and actions permit the development of higher-level patterns of actions. It is these patterns that motivate the players. [*Here again you need to ask questions of subjects: First stage is learning the rules. What this interesting? Was it gratifying to experience that you are learning and mastering the rules?] So that is the first level of gratification: mastering the rules. This is crucial because it gives you a sense of control.

Now, the analogy here is that life is like a game, in that there are agents and actions. In real life, these are not tightly constrained. There may be new agents entering the picture, or there may be so many agents that you have problems tracking what each one may do. There is the combinatorial explosion of possible interactions between agents. As the level of unpredictability rises, you still need to get things accomplished; at a minimum, you need things accomplished. If you need to but cannot predict what other agents will do next, your system will respond by becoming stressed. Games reduce stress levels -- this should be measurable! [*Another research note: design an experiment where you stress subjects, and then ask them to play a game to see if stress-levels fall.]

This is not to suggest that the biological function of games is to lower stress: it is clearly not. We know this because people are also strongly attracted to games that are stressful. [*Research note: document stress in games.] However, the stress you experience in games is constrained to the pretend scenario of the game, and is therefore not persistent and harmful; it can be interrupted at will. In this sense, the lack of control experienced within the game takes place in a pretend space that in itself is completely under control. This makes the stress experienced within a game potentially enjoyable, a part of the game.

In the simplest forms of games, such as board games and card games, the agents and the actions possible are very tightly constrained. A prototypical example is chess: each agent is capable acting in a tightly constrained manner. At the same end of the spectrum are card games. Solitaire games present an interesting analog to The Sims offline: they are played by a solitary individual for pleasure.

Why are such solitary games enjoyable? Our interviews indicate the following:

the player finds it enjoyable to learn and to master the rules

It is worth emphasizing here that it is the mastery and not the task of learning that rules that is enjoyable. The learning itself is experienced as a cost: it is time-consuming to learn the rules, and the game isn't much fun while you are just learning the rules. What is enjoyable is the power you get when you master the rules.

In the Sims, for instance, our subjects found the initial interface aversive, as they didn't know how to use the controls. Once they learned a few controls, they found it enjoyable to apply them to the initial practice situation provided in the Sims. [*Research note: we need to establish this -- I may need to write a diary myself]. Users accept the cost of learning the rules in order to gain access to the mastery they expect to see in the game. This is the first stage.

Mastery itself comes in several stages. At the first level, consider the solitaire games.

Teeclub

In the game teeclub, there are cards from two decks (all agents are known), some of which are laid out in nine colums of five cards each:

The actions available to each card are simple:

cards can move to form descending sequences
same-suit sequences can move together

These are the rules within the main theater of action. There are also rules for introducing new agents, and for removing agents from this theatre:

new cards can be introduced from a face-down deck and added to the first column
cards can be removed from the theater to build eight ascending same-suit stacks

Such "entries" and "exits" of agents are irrevocable.

The actions available to each card are simple:

cards can move to form descending sequences
same-suit sequences can move together

These are the rules within the main theater of action. There are also rules for introducing new agents, and for removing agents from this theatre:

new cards can be introduced from a face-down deck and added to the first column
cards can be removed from the theater to build eight ascending same-suit stacks

Such "entries" and "exits" of agents are irrevocable.

The goal of the game, as in most solitaire games, is to create order out of disorder. The game starts out with scrambled agents and is completed when everyone has found their place in the social hierarchy. In this sense, the game of solitaire is a metaphor of the problem of life, conceived in terms of creating a fixed and pre-determined social order. More abstractly, the task of the games is to create a simple and immediately graspable order out of a complex and hard-to-grasp disorder. The game thus moves from a cognitively complex situation to one that is entirely controlled and predictable.

This is illustrated by the work that is accomplished in the central workspace of the game: cards enter this workspace in random and unpredictable order, typically to the annoyance of the player, who has to create order of out the cards available at any given point in the game, but leave it in a fixed and predictable succession.

These rules are simple, yet the game itself is quite complex. The combinatorial possibilities of two stacks of cards, scrambled into nine columns -- how do you find a measure of this?

The key point here is that the game presents a branching tree of possible actions, whose final outcomes cannot be computed by the human mind. This is a critical feature. The point is not that the outcomes are not knowable; they most certainly are, as the game is entirely deterministic. Rather, the point is that the game has been deliberately constructed to have the following qualities:

only some trees succeed (some trees result in a failed game)
the branching trees of possibilities are too complex for the human mind to track to the final end point
certain configurations are reliably superior (closer to the goal) than others

You could try to formulate the third quality differently: the point is that there is a reliable causal feature of certain configurations that they will lead to a solution, or that incremental change is possible. The idea is that you could have a game where there is only one solution, and this solution requires a very large number of steps. These steps result in configurations that are not visibly closer to the final solution than any other. Rubrick's cube is like this: it is puzzling because the steps involve configurations that on the surface appear to remove you further from the desired solution. So in this card game there are incremental solutions. The reason this matters is that you can develop strategies: the Rubric cube is not suitable for developing strategies.

So this is the point you wanted to arrive at: games are designed in such a way that they lend themselves to strategic thinking.

So this is the key point: games are designed in a manner that is strictly customized to human cognitive abilities: they create problems that are challenging yet solvable. More precisely, they train strategic thinking.

In this sense, games are a science of strategic action. The way in which games differ is the nature of the construction of the theater -- of the characteristics of the agents and their allowable repertoire of actions.

What is strategic thinking?

What is strategic thinking? In textbooks on learning, [* Fill this in later]. Strategic thinking is a methodology for dealing with uncertainty. Now, think about this a little bit. Consider the differences in the way Deep Blue plays chess and Kasparov plays chess. Big Blue simply computes millions of branching trees to their end point and then picks the trees that lead to the predetermined goal. Kasparov thinks strategically.

We value the ability to think strategically higher than the ability to compute all trees to their end points. Why? The obvious answer is that natural selection has somehow favored strategic thinking. Why would this have happened? Because strategic thinking makes optimal use of limited cognitive resources, and because life -- some significant aspect of life -- is structured in such a manner that strategic thinking is possible.

What characterizes situations that permit strategic thinking?

For strategies to be possible, you need a situation that has the following properties:

there must be regularities in behavior that have statistical validity

This suggests that strategic action is a matter of assessing probabilities, but more than that: there has to be the potential for incremental advantage. This means a more fine-grained structure: not just probabilities, but structured hierarchies of probabilities. The idea is that social reality -- including the society of animals -- is structured in such a way that actions are not only moderately predictable, but layered in some way.

Consider this contrasting example. The solitaire card game teeclub is in fact deterministic, or causally closed -- that is to say, all branching trees have finite end points. So in the case of the card game, as in the case of chess, raw computational power will ultimately be more successful than human strategic thinking, simply because the problem space is well-defined and closed.

The problems human beings have faced through evolutionary history don't typcially share these characteristics. No real-world problem belongs in a closed problem space. Some problems are nevertheless well defined: for instance, the problem of moving inanimate objects defines a situation that requires a minimal amount of work. This work, however, can be accomplished in an infinite number of ways; it is open-ended.

What characterizes human interactions is that the problem space is defined by what the other wants, or more simply, by its contingent behavior. The idea here is that if you have information about the animal's goals, you can predict its behavior. So let's say you know that an animal often will travel along a certain path. That's all the information you have. You can then lie in wait for it for days, as the komodo dragon does, hunting goats. Now you don't know the goat is going to come your way, but there is a chance that it will -- all you know is that it often travels this way, that it prefers a certain path, and that you can wait for it. Is this strategic thinking?

In brief, strategies are second-order rules that tell you when to apply first-order rules.

First stage in learning solitaire

Let's return to the solitaire game and look at what we mean by strategic thinking. At the start of the game, scrambled cards are placed in nine colums of five. Inexperienced users first have to learn the rules: form descending sequences, move same-suit sequences together. The first preference rule is simple:

remove cards from the theater

The removal rules are simple: build same-suit stacks in ascending order. This initial strategy quickly comes short in creating order, necessitating the invocation of the second rule:

add cards to the theater

The adding rule is simple: take the top card from the face-down deck and place it last in the first column. This rule also quickly fails to deliver the desired result, as the cards to not appear in the sequence in which they can exit the came. We then move to the rules of engagement within the theater itself:

prefer to build sequences

That is to say, given the choice between adding a new card an building a sequence, build a sequence. This creates an ordered set of actions, or a preferred order of actions:

remove cards from the theater
build all possible sequences
add cards to the theater

This preferred sequence is not in itself part of the rules of the game; instead it represents an ordering of how these rules are applied. So the first take is that strategies are meta-rules that govern how rules are applied. That is to say, in a game, the rules are not recipes of action -- they underspecify what can be done within a game. The rules literally don't tell you want to do, since several rules apply to the situation [structure the paper so that this becomes evident]. The rules don't provide enough information to determine every choice. So the idea is that there is a more general problem, namely that of deciding which rules to apply when. We call the preference systems that tell you which rule to apply when a strategy.

The development and application of strategies depend on the player's ability to maintain a running representation of the affordances of the board -- that is to say, of all the things than can be done on the board at any given time. Failures to update the affordances will lead to the failed application of strategies -- that is to say, to "mistakes" in the game. [* Verify this with players that they label such failures as mistakes.]

This running representation must be kept in working memory. Players that are distracted lose the representation of current affordances and must update it before they resume playing, or they will make mistakes. [*You can likely test players working memory by presenting them with a range of configurations and ask them to identify which configuration is the one they were just working with.]

The initial strategy is very simple: it says move cards out that can be moved, and then build all possible sequences. When new useful sequences can no longer be built, the board is "locked" -- nothing can be moved to advantage. At that point, add a new card.

Second stage of learning: Developing second-order preference rules

Entailed preference rules

There are other strategies that a user might develop after playing the game for a while. Consider this example (fig. 2): there the 6 in the 9th column could host a 5 and a 4, yet the 4 was placed on the 5 before the 5 was moved. You may notice that you have temporarily imprisoned a card by another suit, thus preventing a move that previously was possible. In order to realize this, you must maintain a representation in working memory of what the board looked like one move ago, realize that you have lost a possible move, and then simulate a counterfactual situation in which you did not lose that move but instead made the move. Finally -- and this is the crucial point -- you realize that you lost the move for a completely predictable reason: lower cards imprison other-suit higher cards, while the inverse is not true. This realization represents the formation of a conceptual understanding of a higher-level order within the game, an order that emerges in a reliable manner from the underlying generative order of the game. The insight into this truth can be formulated as a strategy:

prefer to move high cards before low cards

Note that this rule follows logically from one of the basic rules of the game: mixed-suit sequences cannot be moved, so they must be constructed from the top down. The strategy simply spells out a non-obvious entailment of the basic rule, formulating the consequence of this entailment as a strategy, as a preferred course of action.

This is one type of preference rule -- one that follows logically from the basic rules.

Proximal preference rules

Yet there are other rules that formulate strategies that serve to orient a motivational system and creates a proximal goal that by implication is reliably correlated with the distal goal of the game.

Here is a simple rule that at a stroke vastly simplifies the task of the game. This rule could be generalized even further:

prefer to uncover as many cards as possible

This rule is a restatement of the basic "build all possible sequences" rule. Both of these rules are "orientation rules" or rules that apply unless there is reason to do something else. They are default rules that admit to exceptions. As we discuss in more detail below, these rules acquire an emotional dimension. Following them is gratifying, in the sense that there is an experietial component, a subjective phenomenology that marks the successful execution of these strategies as gratifying, and their omission as painful failures. Thus, uncovering a new card becomes a gratifying experience, an incentive within the game: each uncovered card opens up a new possibility space, and therefore uncovering cards functions as a magnet.

This rule helps build long sequences, freeing up more cards. It is a strategic rule, in that it tells you how to apply the basic rules of the game in a particular sequence. Note that these second-order rules can be elaborated only through the operation of simulations that involve more than one move ahead. In the rule above, for instance, you need to scan the table and identify all possible moves; then within this subset you need to identify which of these moves should be made first, namely those that involve the highest cards.

These simulations open up the vast possibility space of the game, made up of a very large number of branching trees. One approach to this possibility space would be to simulate every possible consequence of every move. This is the approach chosen by Deep Blue in playing chess. The key point is that this move is not open to humans; we lack the computational ability to carry this out. More precisely, we lack the working memory resources.

There may be a couple of reasons for the inability of human beings to simulate the changing affordances of the game. The first is that working memory may be in some sense evolutionarily expensive. The other is that the types of problems that humans evolved to solve did not lend themselves to being simulated a large number of steps ahead. R.D. Laing's Knots brings out the limited utility of the ability to simulate human relationships several steps out: the real predictive power drops off rapidly.

Games may be designed the way they are in order to create situations that resemble the type of challenges that the human mind is designed to solve. This would explain why we show little regard for Deep Blue: the ability to compute each possibility tree to its end point is simply not a meaningful option for a human being, and does not represent an interesting approach to the problem [* confirm this in interviews or questionnaire]. Rather, we place a premium on the ability to develop cognitive shortcuts, preference rules, strategies, that allow us to deal with vastly complex situations by determining their higher-level order.

Disambiguating preference rules

There are other cases where the initial strategy fails to resolve all ambiguities, or direct all choices of action. For instance, "build all possible sequences" or its restatement "prefer to uncover as many cards as possible" is an ambiguous rule: sometimes there is one seven, let's say, and two sixes; which six should be used to build a sequence? These types of questions lead to the development of more complex strategies.

Thus, in the case of the two sixes and a seven, we may discover that the game is such that certain patterns will reliably lead us closer to the goal, while others will be less effective in doing so. In this case, the experience of the consequences of the basic rule that same-suit sequences can be moved together leads to the formulation of the following preference rule:

prefer same-suit over mixed-suit sequences

This disambiguates some situations, but not all. What if neither six is the same suit as the seven? In that case,

prefer sequences that allow cards to exit the theater

In this case, if one of the sixes cover an ace, or another card whose turn has come on one of the final stacks, select that six and remove the underlying card from the theater.

What characterizes these secondary strategies is that they involve the simulation of more than a single move. Put differently, they involve an update to the affordances of the board that must be simulated in working memory before they are realized on the board. Moreover, these rules are at times mutually contradictory. For instance, the rule "prefer to uncover as many cards as possible" may conflict with the rule "prefer same-suit over mixed-suit sequences". You may be faced with the choice of building a longer chain of mixed-suit cards or a shorter chain of same-suit cards. Which action do you chose? You could rank the rules in a weighted order of preference -- first, try to build maximally long chains; if given a choice, build same-suit chains.

Yet players quickly move beyond such fixed-rule strategies to ask questions like, "What is better, a mixed-suit chain of five or a same-suit chain of four?" In order to resolve conflicts between second-order strategic rules, and to develop a richer sense of the relative value of each choice, players quickly begin to develop third-order or iterative preference rules.

Iterative or third-order preference rules

In an iterative preference rule, you simulate three or more moves ahead. For instance, extending the rule "prefer sequences that allow cards to exit", you might formulate the following iterative rule:

prefer sequences that allow sequences that allow cards to exit

Following up on our earlier example, let's say you have two sixes and a seven, neither six is of the same suit as the seven, and neither six cover a card that can exit. How do you select which card to move? You may notice that
one of the sixes covers a card that can be added to a sequence, uncovering a third card that can exit.

This preference rule involves an elaborated simulation: in order to execute this rule, the player must imagine what the board will look like (the reference state) when the six has been moved to the seven, and the uncovered card moved into a sequence. This elaborated simulation relies on working memory, and human beings are only capable of holding a limited number of elements in working memory. The strategy is iterative, in that it it involves imagining a series of acts (the moving of cards into sequences) that each require the reference state to be successively updated. It is this combination of tasks that poses a problem for working memory.

If a series of steps can be undertaken without updating a reference state, working memory might handle six to eight places [* here's another experiment]; this is a case of repetition, where a simple sequence must be recalled. In what we propose to define as an iterative simulation, each step involves a change in a second register, namely the part of working memory that tracks the current state of the board. An iterative process thus involves the simultaneous and successive updating of two different registers.

It is easy to see that the task of elaborating the consequences of a particular move will quickly swamp human working memory capacity. [* Do tests on how many steps people in fact bother to simulate.] As capacity is exceeded, accuracy declines. A few steps out, players are likely to make mistakes. For instance, [*give an example here].

The interesting point here is that the practical limitation of working memory capacity precludes heavily iterative preference rules. Instead, iterative preference rules are run in special situations (see below, strategies of the experienced player, first stage). Yet the main point has to be that iterative preference rules are run occasionally to probe for and tentatively verify strategic shortcuts. It is these shortcuts that dominate in the set of strategies adopted by experienced users.

These shortcut strategies are managed through the recruitment of the emotional system.

Emotional mediation

At different points in the game, different levels of immersion produce different emotional responses. While the basic rules of the game is being learned, emotions are associated with mastery or confusion. While the basic order of the game is being probed, emotions are associated with felicitous moves and with the execution of newly developed strategies. When the player has developed a repertoire of tested successful strategies sufficient to bring most games to conclusion, the emotions have begun to encode something very subtle about the game that we might call "movement capital".

Consider this exception to the "prefer to uncover as many cards as possible" rule:

don't bother uncovering kings

This rule is a special type of rule, for a couple of reasons. First, the king is the top value, so it cannot be added to any other card. This may make it less useful to uncover a king early on in the game. However, uncovering a king is useful under certain conditions. One condition is that there is an open queen, in which case the queen can be placed on the opened king. Another condition is that there is an open column that cannot be utilized in a better way. So the rule of assigning a lower preference to uncovering a king is conditional: it applies unless certain special conditions are present.

This conditional rule is also qualified in another direction: how costly is it to uncover the king? If it is not costly, then go ahead and uncover it. This notion of "cost" is a measure you need to formalize (and this whole section should be moved down), as it represents a fairly abstract measure of the relative merit of different moves. A move is costly if it is perceived to utilize a larger share of "movement capital" than it generates. This "movement capital" is a highly abstract quantity; it represents a complex set of cognitive assessments. The assessment processes themselves are in some (large?) part below the threshold of conscious awareness; the output of these processes is an emotion, which represents "movement capital".

Movement capital is an emotional representation of the likelihood that a given move will open up the game, in the sense of making it easier to bring to a successful conclusion. This alludes to the experienced player's sense of the game's stages.

Now, note that the rule "don't bother uncovering kings" is a cognitive shortcut. The default emotional value of uncovering a king is low; it rises only when the player detects the special cases in which kings are useful. This rule does not follow directly as an entailment from the basic rules; instead, it surfaces from the background cognitive processes that extract patterns from the game in the course of playing it.

The rule may in fact be hard to justify; indeed, it may be wrong. Perhaps this rule is merely a special case of a more general rule, "don't bother to uncover cards that have nowhere to go, or on which nothing can be placed", or more succinctly, "don't bother to uncover cards that don't build sequences". Yet the emotional coding is different: it says in effect, "Kings are less likely to be helpful in building sequences than other cards". Having this rule saves the cognitive effort of building the iterative simulation of uncovering the king.

This illustrates that high-level strategies pick up on statistical patterns within the game, mark them emotionally, and use them to allocate scarce cognitive resources. Now that is starting to sound like a real description of human strategic thinking.

Stages of the game for the experienced player

After playing the game for a while, players learn to apply a different set of strategies to different stages of the game, and to determine the endpoints of these stages with increasing precision. It is worth noting that there is nothing in the game rules that identify these pivotal events, but they recur in every game. In brief, the first stage consists of the moves you can make on the initial board, before adding cards. Once you start adding cards, you move into the second stage, although the first few cards can sometimes help you complete the work of the first stage. The end of the second stage is defined by the creation of ordered sequences on the main board; typically at this stage you are only able to build mixed-suit sequence.

Strategies of the first stage

The opening scene is crucial. A highly successful game is possible only if the first column is cleared, and a king is placed there, preferably accompanied by a same-suit queen and jack. This is because kings are column hogs, and free columns represent the key scarcity of this imaginary world. For this reason, the very first moves are typically the ones that require the most advance planning: you need to track the consequences of several iterations of moves, in order to locate the very best opening move. With some luck, you manage to free the first column and place a plantation there; with more, a second king will land on the initial plantation, keeping the otherwise competing kings on top of each other and out of harm's way.

Animation showing the first stage of the game

If you cannot achieve this, the game is off to a bad start. Adding new cards is a horrible experience, as -- in the absence of a free column -- it is generally not possible to integrate new cards into sequences. As the left column increases in length, so does the chance of ending up with an unsolved game. This is emotionally coded as unpleasant. Note the ease with which our emotions code these highly abstract events: there is a goal, and there are events that make that goal harder to reach (unpleasant) or easier (pleasant).

The lesson is also that the game is extraordinarily sensitive to initial conditions; if you are make a single mistake in this first stage, it changes the character of the entire game, as you are extremely likely to end up with a few low cards imprisoned by a subsequent king in the first column. This will hamper your ability to build both sequences and stacks, creating a game that travels further into the realms of disorder before you hopefully manage to turn the tide.

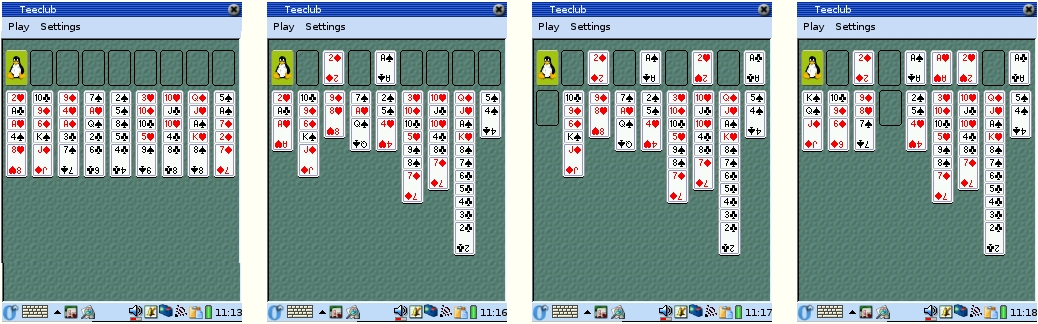
Fig 1: First stage. In this example, the opening scene is extremely favorable, with two aces and a matching two in the feed column. The challenge is to remove both the 8 and the 4. The solution is to uncover both the second and the ninth columns to reach the last card, a 9 and a 5, and in the process free up two aces. Finally, it was then possible to place the king and queen of spades and a jack in the feed column, while leaving an empty column. Since the beginning is so strong, the low clubs are not exited; the goal is to keep the maximum number of cards on the table.

Strategies of the second stage

In the second stage, your focus is not primarily to integrate new cards -- your ability to do this is often limited -- but to clean up your columns. Columns can be disordered in two ways: it can lack sequences, and it can contain multiple suits. As long as you have unordered cards at the heads of columns ("prisoners"), your focus needs to be to get free those rather than to incorporate new cards. This means that your focus in the second stage is to free up and keep free as many columns as possible, since you need several free places to be able to shift mixed-suit sequences about. [* Show a screen shot of this.] Up to three and even four free columns are optimal in this stage, even if they come at the cost of buildup in the first column.

In this second stage, you might use the following advanced strategies. Advanced player discover that there are cases where the initial rules can be violated to advantage. For instance, in the second stage, the player discovers that if he allows the first column to grow too large, there will be cases where he is unable to recover. That is to say, he associates a long first column with a cost, an expenditure of a finite movement capital. This leads him to avoid lengthening the first column whenever possible, and to divide the board into two parts: the first column and the main board.

Advanced players discover that there are times when the first column is a useful place to store cards, and thus free up the movement of the main board. This involves moving cards from the main board to the first column when circumstances warrant. This is done with a clear sensibility of the cost: moving cards from the main board to the first column should have a clear payoff.

This strategy can then be incorporated into planning. Thus, in a particularly locked main board, a player may add several new cards while looking for a particular card that can be used to offload the main board.This is sometimes the only way to unlock a stuck board.

Another strategy is "do it if you'll be no worse off from doing it". This is useful in situations where, for instance, you need to temporarily occupy a free column. By repeating this maxim, you can free up your emotional reluctance to occupy the column. In most cases, such a reluctance is warranted, as mistakes are costly in this case. Yet if it is clear you'll be no worse off, go ahead and reap the fruits. A smart move to the first stack can clear the field and allow the remaining stacks to organize, freeing up several columns.

If, in the first stage, you managed to imprison a king and court at the head of the first column, your work in the second stage of freeing prisoners on the main board will have been made significantly easier.

Strategies of the third stage

What marks the end of this second stage is the point where you have cleaned up all your columns. At that point, your strategies can shift: once you have no more prisoners, can focus on integrating cards from the first column into the main board. This means there is no longer a premium on keeping several free columns; you will normally have enough mobility now with a single free column, and even that could in special cases be utilized to leave a card in. As you shift to third-stage strategies, you are rapidly incorporating new cards into sequences, and using every opportunity to lengthen your same-suit sequences. In this second stage, it is the frequency of same-suit sequences that determines your freedom of movement, just as it was the availability of free columns in the second stage. You learn various tricks to shift your sequences into the same suits; for instance, if you have several columns that end in adjascent values, it is easier to move the ends of columns arount. Completed columns -- columns that reach down to the lowest values, are hard to shift around and cannot provide help to their neighbors.

In this sequence, we see the easy work of the second and third stages when the first stage is successful. Three and even four columns are kept open in the second stage, and most of the cards can be left in place in the final stage.

Shifting the goal of the game

If in the first stage you were able to imprison a king in the first column, and your second stage was completed without having to accumulate a large number of cards in the first column, you may have created so much movement capital that the original goal of the game, to create ordered stacks, has become too easy. In this case, you can simply shift the goal of the game to keep as many cards as possible on the board. Success can then be measured in the count of cards in the final stacks at the point when all the columns are fully ordered. [* Show a screenshot.] The virtue of this final shift in the very goal of the game is that the game remains challenging even when things are going really well.

Notice that this new goal invalidates basic preference rules of the game, as elaborated above: "prefer sequences that allow sequences that allow cards to exit" is no longer valid.

Given this new goal, you will find yourself, in all stages of the game, attempting to keep cards on the table rather than removing them to the stacks. This makes the game slightly harder; however, it is almost always easy to back off on this higher level of ambition and exit the cards that are able to exit in order to make room for new cards. That is to say, the new goal is not irrevocable; it can be fluidly combined with what remains the overarching goal, which is to create order.

Summary

This examination of the game shows that a simple solitaire game forces the player to develop strategies. These are second-order rules for when to apply first-order rules. Strategies are sensitive to context; they depend on maintaining an overall view of the current situation in working memory. Each second-order rule is formulated on the basis of an insight into the underlying order of the game, and this insight is expressed in the form of a strategy of action. Some strategies are simply the entailments of the basic rules. The vast majority of strategies, however, are high-level preference rules that pick up on statistical patterns within the game, mark them emotionally, and use them to allocate scarce cognitive resources.